Teoria Del Gioco Parte 1

La teoria del gioco è un ramo della matematica che si occupa del processo decisionale nelle situazioni in cui due o più giocatori hanno interessi concorrenti. Viene spesso usata in economia e in biologia, ma può essere usata anche nel poker. Al fine di spiegare il concetto inizieremo in modo facile, il che significa che in questo articolo non si parlerà molto di poker. Inizieremo applicando il concetto al gioco nella Parte 2 una volta che avremo le basi. Il più noto esempio di teoria del gioco è il dilemma del prigioniero. Molti di voi conosceranno già questo esempio, ma per quelli di voi che non lo conoscono lo spiegherò ancora una volta.
Da qualche parte viene commesso un crimine e la polizia arresta due uomini. La polizia è sicura che questi due uomini hanno commesso il crimine, ma non ha le prove per dimostrarlo. Poi uno di loro ha una grande idea. Decidono di spostare i prigionieri in camere separate e di fare a ciascuno la stessa proposta. Possono tradire il loro partner e passare meno tempo in galera o possono entrambi rimanere in silenzio. Se nessuno dei due prigionieri dice qualcosa, la polizia non ha prove ed entrambi rimarranno in galera un anno per possesso di pistola. Se uno dei due parla e l'altro rimane in silenzio, il primo sarà libero mentre il suo partner andrà in prigione per 10 anni. Se entrambi i prigionieri parlano, entrambi andrebbero in prigione per 8 anni (non 10 perchè entrambi hanno aiutato con l'investigazione).
Possiamo presentare tali informazioni in una tabella come segue:
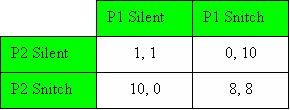
Questa tabella viene chiamata "matrice dei profitti", e in essa vediamo i possibili risultati per i due giocatori in gioco. Il primo numero è sempre il risultato per il prigioniero 1 (P1), e il numero dopo la virgola è il risultato per il prigioniero 2 (P2). Se entrambi tacciono, entrambi vanno in prigione per 1 anno. Se uno parla e l'altro tace, uno andrà in prigione per 10 anni e l'altro sarà libero. Se entrambi parlano, entrambi andranno in galera per 8 anni. L'esito che la polizia preferirebbe è quello in cui entrambi si tradissero a vicenda, in quanto le strade sarebbero al sicuro da questi due criminali. La polizia tuttavia è fortunata, perchè nel modo in cui ha impostato questa situazione, entrambi i prigionieri parleranno sempre. Perchè ciò accade?
Beh, immaginiamo di essere P1. Sei seduto nella tua cella a pensare a cosa fare, e non sei sicuro su cosa farà P2, in quanto non hai alcun modo di comunicare con lui. Così pensi a tutte le cose che potrebbero succedere. Mettiamo che P2 parli. In quel caso sarebbe meglio parlare anche per te, in quanto faresti meno prigione se lo facessi. Mettiamo che P2 non parli. In questo caso è sempre meglio per te parlare, in quanto non andresti neanche in galera. In sostanza non importa cosa fa P2, perchè per te sarà sempre meglio parlare. Per P2, la situazione è esattamente la stessa, anche per lui sarà sempre meglio parlare. Magari P1 pensa: "forse non dovrei dire niente e sperare che P2 faccia lo stesso, in questo caso andremmo fuori entrambi dopo un anno". Ma se P2 poi decide di parlare, tu andresti in prigione per 10 anni! Vuoi prendere questo rischio? Generalmente preferiresti di no, quindi alla fine di questo "gioco", entrambi i prigionieri finiranno per andare in prigione per 8 anni.
Questa situazione viene chiamata Equilibrio di Nash, che prende il nome dal grande matematico John Forbes Nash. Potete trovare maggiori informazioni su di lui nel grande film A Beautiful Mind. Questo equilibrio afferma che nessun giocatore può aggiustare la propria strategia per trarne profitto. Questo è esattamente ciò che i due prigionieri hanno di fronte. Immaginate di essere nell'equilibrio di Nash e che entrambi i prigionieri parlano e vanno in prigione per 8 anni. P1 può cambiare la sua strategia e restare in silenzio, ma poi deve andare in prigione per 10 anni. Non vince niente. Lo stesso vale per P2. Nessun giocatore può trarre profitto qui cambiando la propria strategia.
Ci sono innumerevoli altri esempi di questo. Per esempio, una guerra tra due paesi. Un paese può scegliere di andare in guerra o di non andare in guerra. L'altro paese ha le stesse opzioni. Se entrambi decidono di non andare in guerra, entrambi mantengono le proprie terre al sicuro. Se il paese A va in guerra ma il paese B no, allora A otterrà delle terre extra e B soffrirà le perdite. Se il paese B va in guerra e A no, allora B guadagna terre e A ci perde. Se entrambi vanno in guerra allora entrambi subiranno delle perdite. Ancora una volta possiamo presentare queste informazioni nella tabella matrice dei profitti. Se un paese non subisce attacchi e mantiene le proprie terre intatte, il paese riceve un punteggio pari a 0. Terre extra danno un punteggio di 10 mentre le perdite -10. Alcune perdite danno -5
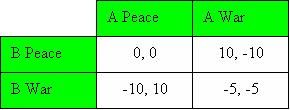
Come potete vedere anche in questo caso è meglio per entrambi i paesi andare in guerra, qualsiasi sia la strategia dell'altro. Immaginate di essere il paese A. Se il paese B attacca, potete decidere di non fare niente (-10) o contrattaccare (-5). Il contro attacco è sicuramente l'opzione migliore in quanto riduce le perdite. Se il paese B non attacca allora A può scegliere la pace (0) o la guerra (10). Ancora, la migliore opzione per il paese A è di andare in guerra. Il paese B è esattamente nella stessa situazione. Questo è il motivo per cui i paesi andranno sempre in guerra, ed è chiamato equilibrio di Nash.
La NATO ovviamente sta cercando di mantenere il mondo un posto pacifico. Come soluzione per il problema nell'esempio sopra, la NATO potrebbe dire ad entrambi i paesi: "Se attacchi l'altro paese ti bombardiamo". Se la NATO decide di bombardare un paese, quel paese subirà grosse perdite. Questo modificherebbe la matrice dei profitti nel modo seguente:
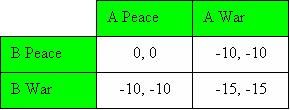
Ora la situazione cambia per entrambi i paesi. Immaginiamo nuovamente di essere il paese A. Il paese B può attaccare e A decide per la pace (-10) o per la guerra (-15). Ora la pace è la scelta migliore. Se il paese B ora sceglie la pace, anche A può scegliere la pace (0) o la guerra (-10). Ancora la pace è l'opzione migliore. In questo nuovo esempio l'equilibrio di Nash sarebbe la pace per entrambi i paesi. Il coinvolgimento della NATO ha modificato con successo la matrice dei profitti per entrambi i paesi, risultando nella pace.
Passiamo ora a esaminare un esempio che ha un po' più a che fare con il poker. Il gioco si chiama Pari e Dispari e consiste in due avversari i quali, nello stesso momento, devono prendere una decisione. Entrambi i giocatori ricevono una moneta e possono decidere entrambi se tenerla oppure no in mano. Ad un certo momento, ad entrambi i giocatori viene chiesto di aprire la loro mano, e se il numero totale delle monete è uguale a 0 o 2, il giocatore A vince, mentre se è uguale a 1, vince il giocatore B. Il vincitore riceve un punteggio di +1 e il perdente di -1. In una tabella matrice dei profitti verrebbe fuori come segue:
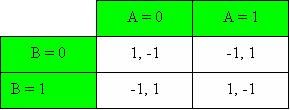
Questo gioco è un gioco a somma costante. Questo è dovuto al fatto che la somma dei risultati nella tabella è sempre pari a una costante, in questo caso 0. In questo esempio è evidente che il giocatore A deve cercare di fare sempre la stessa cosa del giocatore B, in questo modo ci saranno sempre 0 o 2 monete che appaiono e A vince. Il giocatore B deve cercare di far sempre l'opposto di ciò che fa il giocatore A, in quanto ci sarà sempre 1 moneta che appare e il giocatore B vince.
I due giocatori possono provare e cercare modelli nel gioco del loro avversario e reagire di conseguenza. In questo caso, il giocatore più bravo a scoprire questi modelli vincerà la partita. Ma c'è anche un'altra opzione. Mettiamo che sei il giocatore B e credi di essere un giocatore peggiore del giocatore A. Cosa puoi fare a riguardo?
Supponiamo che decidi di girare 0 monete un X% delle volte e 1 moneta un (1-X)% delle volte. Il giocatore A è un giocatore migliore, sa leggere i nostri modelli e sceglierà una certa opzione il 100% delle volte. Supponiamo di decidere di girare 0 monete il 75% delle volte e 1 moneta il 25% delle volte, quindi X = 0.75 e X-1 = 0.25. Il giocatore A non ci metterà molto a capire questo modello e deciderà di girare 0 monete il 100% delle volte al fine di massimizzare il suo EV. Perchè? Beh, ecco la formula EV per il giocatore A:
EV(A) = (1)(X)(Y) + (1)(1-X)(1-Y) + (-1)(X)(1-Y) + (-1)(X-1)(Y)
Dove Y è la percentuale delle volte che A gira 0 monete e X è la percentuale con cui noi (giocatore B) giriamo 0 monete. La formula potrebbe apparire complicata ma non lo è davvero in realtà. Il giocatore A riceve sempre un punteggio di +1 se fa la stessa cosa che fa il giocatore B, e riceve un punteggio di -1 se fa il contrario. Dato che A è più bravo di noi, sa che X = 0.75 e 1-X = 0.25 e può includere questo nella sua formula EV:
EV(A) = (1)(0.75)(Y) + (1)(0.25)(1-Y) + (-1)(0.75)(1-Y) + (-1)(0.25)(Y)
EV(A) = 0.75Y + 0.25 – 0.25 Y – 0.75 + 0.75Y – 0.25Y
EV(A) = Y – 0.5
Ora tutto ciò che il giocatore A deve fare è decidere sul valore di Y. Se sappiamo che Y deve essere tra 0 e 1 (in quanto essa rappresenta una percentuale), diventa evidente che la formula è ottimale per il giocatore A quando Y = 1. Il suo EV è quindi pari a 1 – 0.5 = 0.5. E questo è effettivamente corretto. Se A decide di giocare Y = 1 e gira 0 monete il 100% delle volte, vincerà il 75% delle volte ricevendo un punteggio di +1 e perderà il 25% delle volte ricevendo un punteggio di -1. Insieme, questo ci dà: (0.75)(1) + (0.25)(-1) = 0.5.
Ora supponiamo che noi (giocatore B) facciamo l'esatto opposto, quindi X = 0.25 e 1-X = 0.75. Se ora guardiamo la formula EV del giocatore A, otteniamo ciò che segue:
EV(A) = (1)(0.25)(Y) + (1)(0.75)(1-Y) + (-1)(0.25)(1-Y) + (-1)(0.75)(Y)
EV(A) = 0.25Y + 0.75 – 0.75Y - 0.25 + 0.25Y -0.75Y
EV(A) = -Y + 0.5
Questa è la formula EV del giocatore A dopo aver scoperto il nostro betting pattern, ossia il modello con cui puntiamo, e ancora Y deve essere tra 0 e 1. Possiamo vedere che il suo EV è più grande quando Y = 0, in quanto il suo EV sarebbe quindi pari a 0.5.
Quindi, ciò che il giocatore A fa è, prima di tutto, scoprire la nostra strategia (perchè è più bravo di noi) e calcolare la nostra X per quindi inserire questo valore nella sua formula EV. Quindi sceglie un valore per Y che ottimizza il suo EV e ciò sarà sempre 0 o 1, sulla base della strategia del giocatore B. Il giocatore A perciò sceglierà sempre di fare una certa azione il 100% delle volte, perchè conosce la nostra strategia grazie al suo vantaggio in termini di abilità.
Per questo vantaggio, il giocatore A sceglierà sempre la strategia ottimale contro di noi. Diventa così la nostra Nemesi. La Nemesi conosce sempre la nostra strategia e sceglie sempre la migliore contro-strategia per massimizzare il proprio EV, mentre noi come giocatore B non prendiamo sonno la notte in quanto ci sembra di non riuscire a vincere mai. Ma il giorno dopo ci svegliamo con nuove speranze. Andiamo in cerca di una strategia migliore per noi, sapendo che il giocatore A reagirà sempre con una strategia che massimizzi il suo EV.
Se noi (giocatore B) decidiamo di girare 0 monete più del 50% delle volte il nostro EV è:
EV(B) = (-1)(X) + (1)(1-X)
EV(B) = 1 – 2X
Dato che ci aspettiamo che il giocatore A giri 0 monete il 100% delle volte (perchè è più bravo di noi e conosce il nostro betting pattern) se giriamo 0 monete un X% delle volte, il giocatore A girerà anche lui 0 monete e riceverà un punteggio di +1, mentre noi otteniamo un punteggio di -1. Il restante (1-X)% delle volte, noi gireremo una moneta, A non girerà una moneta perchè è la sua strategia ottimale, e noi otteniamo un punteggio di +1.
Se decidiamo quindi di girare 1 moneta più del 50% delle volte, il nostro EV è:
EV(B) = (1)(X) + (-1)(1-X)
EV(B) = 2X – 1
Dato che ci aspettiamo che il giocatore A giri sempre 1 moneta qui, (perchè è più bravo di noi e conosce il nostro betting pattern) se giriamo 0 monete un X% delle volte, il giocatore A girerà 1 moneta (perchè questa è la sua strategia ottimale), e noi vinciamo e otteniamo un punteggio di +1. Il restante (1-X)% delle volte in cui giriamo una moneta, e A farà lo stesso vincendo, noi otteniamo un punteggio di -1.
Il nostro EV, pertanto, dipende da X. Ricorda che X è uguale alla percentuale delle volte che noi giriamo 0 monete. Ora abbiamo anche due formule EV differenti per due strategie differenti. La strategia 1 implica che giriamo 0 monete più del 50% delle volte e la nostra formula EV quindi è: EV = 1 – 2x. La strategia 2 implica che giriamo 1 moneta più del 50% delle volte e la nostra formula EV è quindi: EV = 2x – 1.
Mettendo queste due formule in un grafico otteniamo:
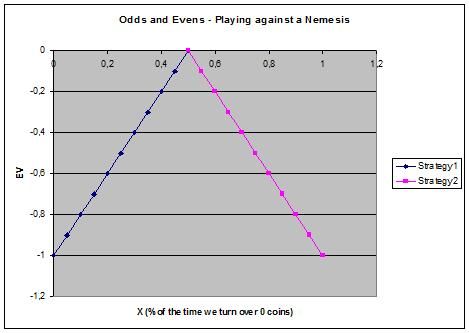
Da questa tabella si può vedere che per noi (giocatore B), la strategia ottimale è girare 1 moneta il 50% delle volte e girarne 0 il restante 50% delle volte. Anche se questa conclusione potrebbe sembrare logica per molti di voi, spesso calcolare tali risultati può essere complicato. Quando avrete a che fare con situazioni più complesse sarà molto utile conoscere l'effettivo processo di come giungere a queste conclusioni. La strategia 1 è possibile per X = 0.5 a X = 1, e la strategia 2 è possibile per X = 0 a X = 0.5. Entrambe le strategie raggiungono il loro ottimale a X = 0.5, dove EV = 0. Dato che per ogni altro valore di X il nostro EV è negativo, possiamo contrastare il giocatore A facendo ogni giocata il 50% delle volte. Il giocatore A non è più nella posizione di sfruttare il suo vantaggio in termini di abilità. Egli ora può fare ciò che vuole, non sarà mai in grado di raggiungere un EV superiore di 0, e noi avremo neutralizzato con successo il suo vantaggio.
Questo esempio mostra come la teoria del gioco può neutralizzare il vantaggio in abilità del tuo avversario. Questo metodo può anche essere usato per aiutare il tuo gioco nel poker, ma è qualcosa di cui parleremo nella parte 2.
Mi auguro abbiate trovato questo articolo interessante. Come sempre, domande, commenti e critiche sono sempre più che benvenute nel forum.









